How To Solve Implicit Differentiation In Two Steps ? | Entry Test Trick

How To Solve Implicit Differentiation In Two Steps ? | Entry Test Trick

How To Solve Implicit Differentiation In Two Steps ? | Entry Test Trick 

In Order to Solve Differential Equations in Which X and Y variables cannot be separated easily or sometimes, it becomes impossible for us to Solve them in a few steps. In Entry Tests, Time is Important factor. Therefore, Taleem Tutor Brings for You A Short Cut To Solve Lengthy Questions Easily In Two To Three Steps. Lets review definition of implicit equations:

An Equation Which cannot be expressed independently in terms of x and y variables.

For Example:

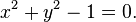
  • The implicit equation of the unit circle is  x^2 +y^2-1 = 0.
  •  x2 y3 + x3 y2 
  •  x2 y3 + x y2 + x3 y2 

How To Solve in Two To Three Steps?

Steps:
  1. Write the Whole Equation on One Side of Equals Sign.
  2. First Differentiate the Function with respect to x considering y as a constant. (equation 1)
  3. Then Differentiate the Function with respect to y considering x as a constant. (equation 2)
  4. Divide (equation 1) by (equation 2) and multiply by -1.
  5. Simple Formula is Given Below
  6.  

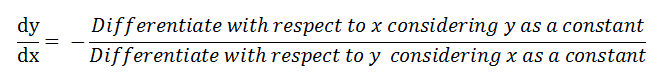
Lets Have an Example:


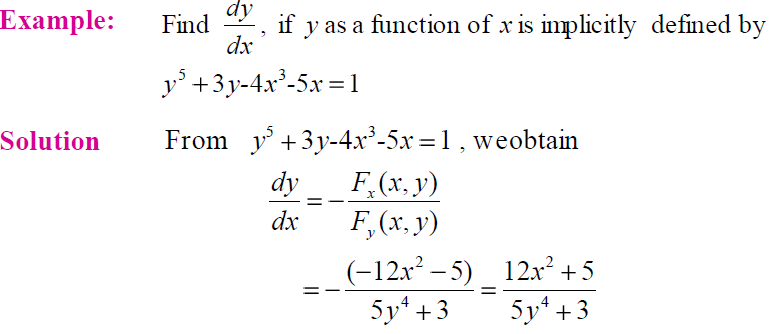
Want Practice Questions?

Here You Go >>  From Text Book of FSC




Share on Google Plus
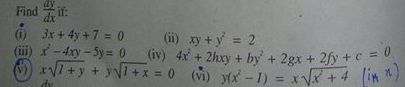
    Blogger Comment
    Facebook Comment